operna_zed_freet

Opěrná stěna

In [10]:
from __future__ import print_function

import openturns as ot
from openturns.viewer import View
import math as m
from collections import OrderedDict
import re
import matplotlib.pyplot as plt
No description has been provided for this image

Výpočet

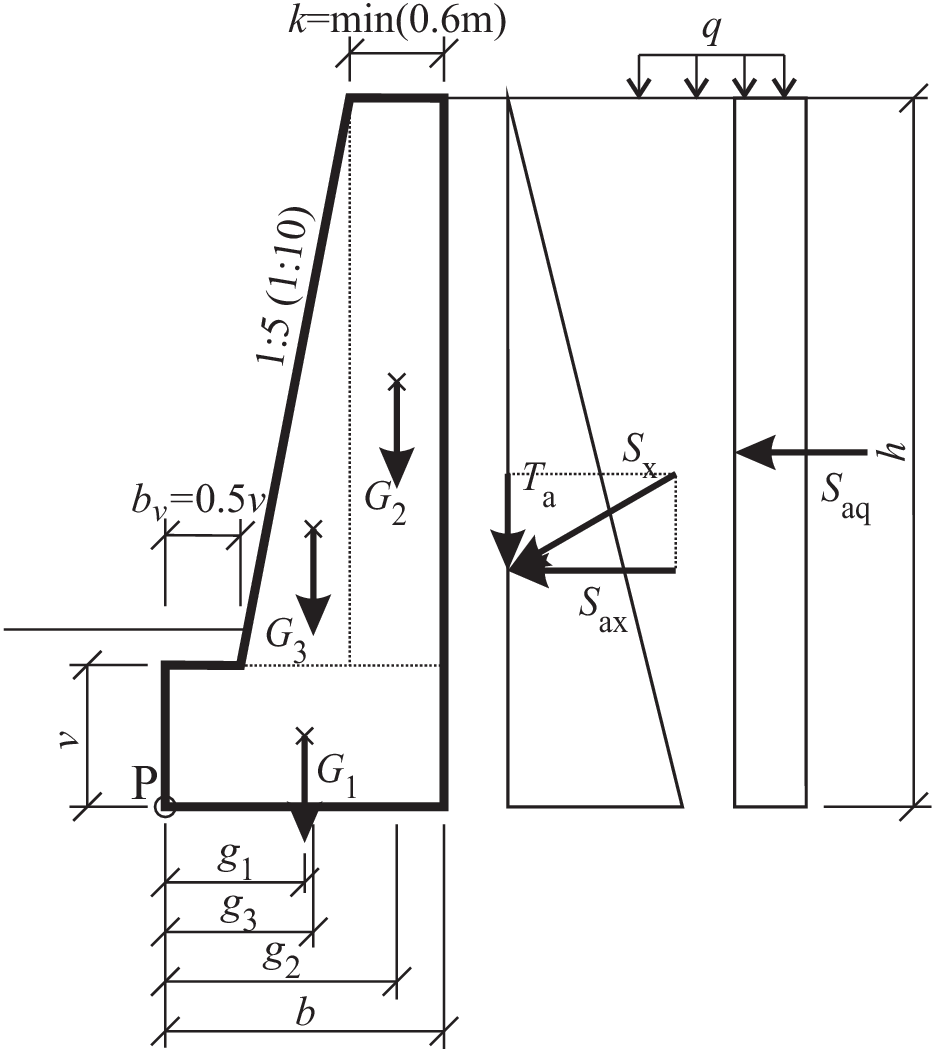
Posouzení opěrné stěny na únosnost v základové spáře provedeme podle následujícího postupu a uvedených vzorců. Označení geometrických rozměrů a sil je zřejmé z obrázku. Stěna je rozdělena na tři geometrické části, pro které vypočítáme vlastní tíhu a polohu těžiště od přední hrany základu (bod P) podle následujících vztahů: \begin{equation}\nonumber G_1 = v b \gamma_{\rm m} \quad G_2 = k \left( h-v \right) \gamma_{\rm m} \quad G_3 = \frac{1}{2}\left( h-v \right)\left( k + \frac{h}{10}\right)\gamma_{\rm m} \end{equation}

\begin{equation}\nonumber G = G_1 + G_2 + G_3 \end{equation}

\begin{equation}\nonumber g_1 = \frac{1}{2} b \quad g_2 = b - \frac{1}{2} k \quad g_3 = b_v + \frac{2}{3}\left( b - b_v -k \right) \end{equation}

Dále si vypočteme síly od zatížení zeminou, budeme uvažovat pouze aktivní zemní tlak za rubem stěny (pasivní tlak zeminy před konstrukcí stěny zanedbáme). Výslednice horizontálního účinku aktivního zemního tlaku působící na stěnu v jedné třetině výšky $h$: \begin{equation}\nonumber S_{\rm ax} = \frac{1}{2} \gamma_{\rm z} h^2 K_{\rm a} \qquad K_{\rm a} = \tan^2 \left( 45^\circ - \frac{\varphi}{2} \right) \end{equation} Výslednice od spojitého přitížení za rubem stěny v jedné polovině výšky $h$: \begin{equation}\nonumber S_{\rm aq} = q K_{\rm a} h \end{equation} Svislý účinek zeminy na stěnu: \begin{equation}\nonumber T_{\rm a} = S_{\rm ax} \tan{\delta} \qquad \delta = \left( \frac{1}{2} \div \frac{1}{3} \right) \varphi \end{equation} Moment k bodu P působící na stěnu: \begin{equation}\nonumber M_{\rm a} = G_1 g_1 + G_2 g_2 + G_3 g_3 - \frac{1}{3} h S_{\rm ax} - S_{\rm aq} \frac{h}{2} + T_{\rm a} b \end{equation} Svislá výslednice působící na základovou zeminu: \begin{equation}\nonumber V = G + T_{\rm a} %H = S_{\rm ax} \quad \end{equation} Efektivní plocha mezi základem a zeminou: \begin{equation}\nonumber A_{\rm ef}=b_{\rm ef} \cdot 1 = (b - 2e)\cdot 1 \quad e = \frac{1}{2} b - a \quad a = \frac{M_{\rm a}}{V} \end{equation} Posouzení únosnosti v základové spáře provedeme podle následující nerovnosti: \begin{equation}\nonumber \sigma = \frac{V}{A_{\rm ef}} < R, \end{equation} kde $\sigma$ je napětí v základové spáře od zatížení působícího na stěnu, které musí být menší než únosnost základové půdy $R$. Únosnost základové půdy budeme pro zjednodušení uvažovat jako náhodnou veličinu zadanou pomocí pravděpodobnostního rozdělení.

Náhodné veličiny

Všechny náhodné veličiny jsou uvažovány nezávislé.

Freet Name Distribution Mean Std CoV min max
x1 $k$ Deterministic 0.8
x2 $\gamma_{\rm m}$ Normal 24 1.2 0.05
x3 $q$ LogNormal 4 0.4 0.1
x4 $\varphi$ Truncated Normal 33 4.95 0.15 31 36
x5 $\gamma_{\rm z}$ Normal 20 2 0.1
x6 $R$ Lognormal 315 37.8 0.12

Vygenerování funkce dosazením všech mezivýpočtů do výsledné rovnice

In [13]:
d = OrderedDict(
    k = 'x1', # sirka na vrcholu steny
    gamma_m = 'x2', # objemova tiha materialu steny
    q = 'x3', # spojite zatizeni za stenou
    phi = 'x4', # uhel vnitrniho treni
    gamma_z = 'x5', # objemova tiha zeminy
    
    h = '6.0', # vyska steny
    v = '1.2', # vyska zakladu
    sklon = '5', # sklon lice steny 1:5 az 1:10

    # vypocet pomocnych hodnot pro vypocet napeti
    # v zakladove spare od zemniho tlaku 
    # a spojiteho pritizeni za gravitacni stenou
    bv = '0.5 * v', # sirka predsazeni zakladu
    b = 'k + bv + h / sklon', # sirka zakladu

    G1 = 'v * b * gamma_m',
    G2 = 'k * (h - v) * gamma_m',
    G3 = '1 / 2.0 * (h - v) * (k + h / sklon) * gamma_m',
    G = 'G1 + G2 + G3', # vlastni tiha steny

    # ramena vlastnich tih k bodu P
    g1 = '1 / 2.0 * b',
    g2 = 'b - 1 / 2.0 * k',
    g3 = 'bv + 2 / 3.0 * (b - bv - k)',

    # soucinitel aktivniho zemniho tlaku
    K_a = '(tan((45.0 - 0.5 * phi) / 180.0 * pi))^2',

    # sila od zemniho tlaku
    S_ax = '0.5 * gamma_z * h ^ 2 * K_a',
    S_aq = 'q * K_a * h',

    # zanedbano
    delta = '1/2.0 * phi',# 1/3 az 1/2 * phi 
    T_a = 'S_ax * tan(delta /180. * pi)',


    V = 'G + T_a',
    M = 'G1 * g1 + G2 * g2 + G3 * g3 - S_ax * h / 3.0 - S_aq * h / 2.0 + T_a * b',
    a = 'M / V',
    e = '1 / 2.0 * b - a', # excentricita
    A_ef = 'b - 2.0 * e', # efektivni plocha

    # napeti v zakladove spare
    #sigma_v = 'V / A_ef'
)

sigma_v = 'V / A_ef'
In [14]:
for i in list(d.keys())[::-1]:
    sigma_v = re.sub(r'([ (]+)(%s)([ ),]+)' % i, r'\1(%s)\3' % d.get(i), sigma_v)
    sigma_v = re.sub(r'^%s ' % i, r'(%s) ' % d.get(i), sigma_v)
    sigma_v = re.sub(r' %s$' % i, r' (%s)' % d.get(i), sigma_v)
print(sigma_v)

((((1.2) * ((x1) + (0.5 * (1.2)) + (6.0) / (5)) * (x2)) + ((x1) * ((6.0) - (1.2)) * (x2)) + (1 / 2.0 * ((6.0) - (1.2)) * ((x1) + (6.0) / (5)) * (x2))) + ((0.5 * (x5) * (6.0) ^ 2 * ((tan((45.0 - 0.5 * (x4)) / 180.0 * pi))^2)) * tan((1/2.0 * (x4)) /180. * pi))) / (((x1) + (0.5 * (1.2)) + (6.0) / (5)) - 2.0 * (1 / 2.0 * ((x1) + (0.5 * (1.2)) + (6.0) / (5)) - ((((1.2) * ((x1) + (0.5 * (1.2)) + (6.0) / (5)) * (x2)) * (1 / 2.0 * ((x1) + (0.5 * (1.2)) + (6.0) / (5))) + ((x1) * ((6.0) - (1.2)) * (x2)) * (((x1) + (0.5 * (1.2)) + (6.0) / (5)) - 1 / 2.0 * (x1)) + (1 / 2.0 * ((6.0) - (1.2)) * ((x1) + (6.0) / (5)) * (x2)) * ((0.5 * (1.2)) + 2 / 3.0 * (((x1) + (0.5 * (1.2)) + (6.0) / (5)) - (0.5 * (1.2)) - (x1))) - (0.5 * (x5) * (6.0) ^ 2 * ((tan((45.0 - 0.5 * (x4)) / 180.0 * pi))^2)) * (6.0) / 3.0 - ((x3) * ((tan((45.0 - 0.5 * (x4)) / 180.0 * pi))^2) * (6.0)) * (6.0) / 2.0 + ((0.5 * (x5) * (6.0) ^ 2 * ((tan((45.0 - 0.5 * (x4)) / 180.0 * pi))^2)) * tan((1/2.0 * (x4)) /180. * pi)) * ((x1) + (0.5 * (1.2)) + (6.0) / (5))) / ((((1.2) * ((x1) + (0.5 * (1.2)) + (6.0) / (5)) * (x2)) + ((x1) * ((6.0) - (1.2)) * (x2)) + (1 / 2.0 * ((6.0) - (1.2)) * ((x1) + (6.0) / (5)) * (x2))) + ((0.5 * (x5) * (6.0) ^ 2 * ((tan((45.0 - 0.5 * (x4)) / 180.0 * pi))^2)) * tan((1/2.0 * (x4)) /180. * pi))))))
In [ ]: